Tag: ATPL
-
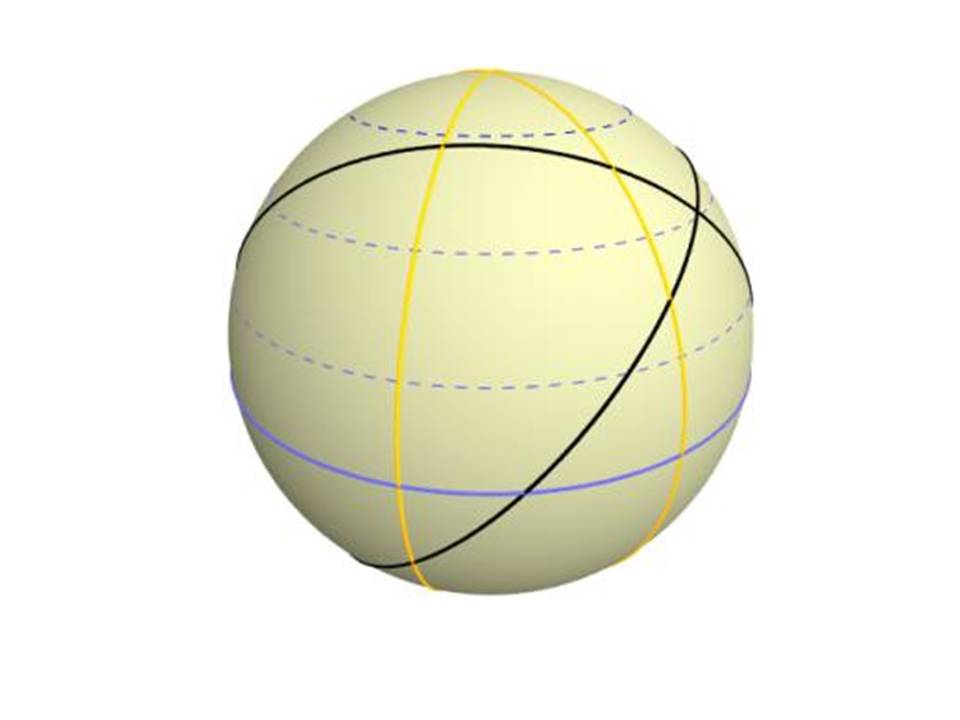
Geval 4 - EASA ATPL General Navigation berekeningen tussen twee "willekeurige" punten: Vind de driehoek
Als u voor een EASA General navigation examenvraag de track en/of afstand wilt berekenen zonder de klassieke grootcirkelformules te gebruiken en nadat alle andere snelkoppelingen hebben gefaald, moet u de driehoek vinden in de lijnen die de twee coördinaten verbinden.
-

Geval 3 voor GNAV twee "willekeurige" punten: Als A en B op dezelfde breedtegraad liggen
Part 3 in the series about Calculating tracks and distances between two not so random points On the bottom of this post you can try your luck with two ATPL questions for this case. The plot thickens. You must have arrived here because the answer to the two previous questions is “no”. Case 1: Same…
-

Geval 2 voor GNAV twee "willekeurige" punten: A en B liggen op de anti-meridiaan
If case 1 is not true then try this: Question 2:Are A and B on each other’s anti-meridian? Anti-meridians are two meridians exactly 180 degrees apart that connect a great circle around the globe. Example: A: 40N 120EB: 10N 060W
-
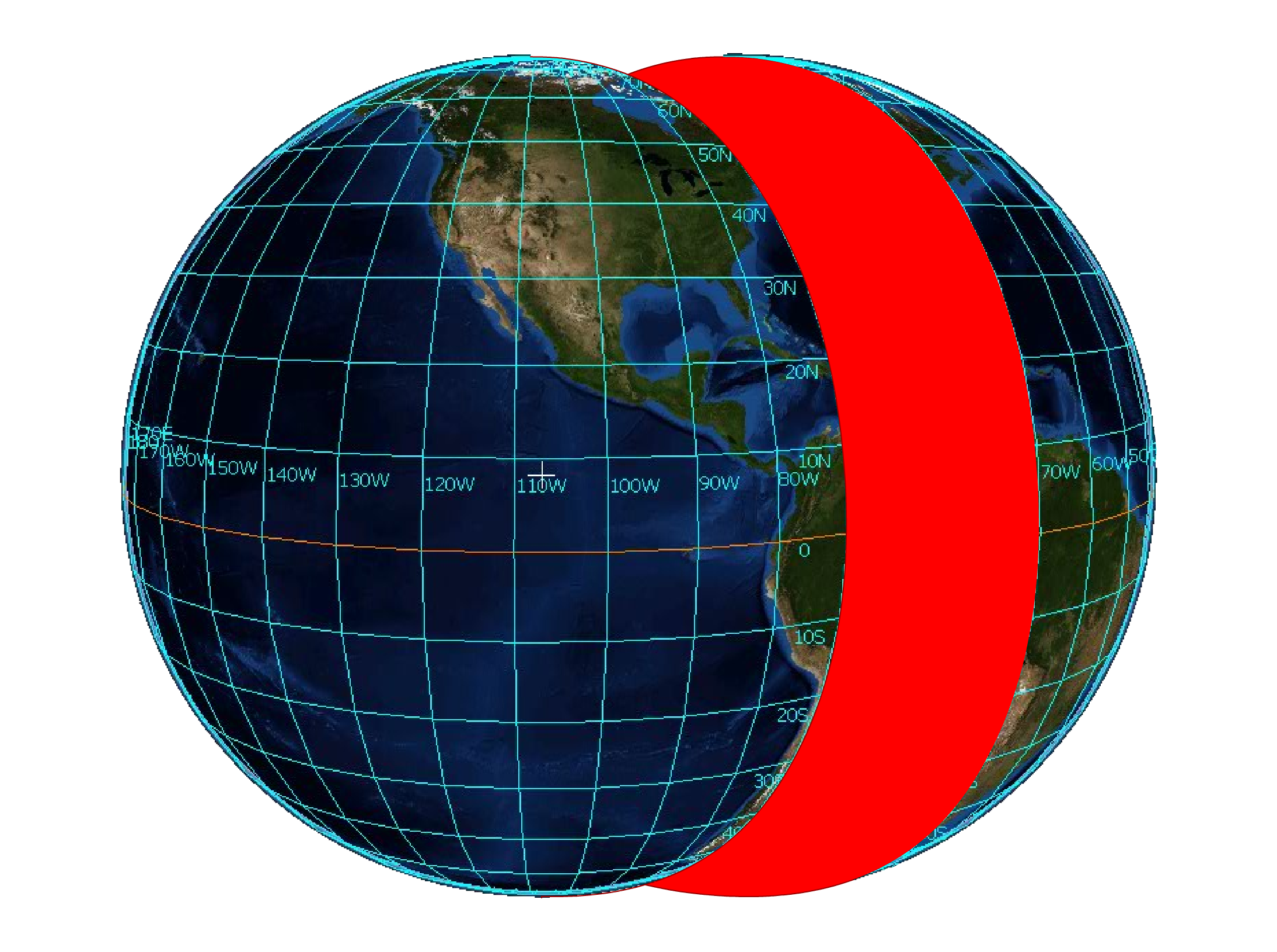
Geval 1 voor GNAV twee "willekeurige" punten: A en B liggen op dezelfde meridiaan
Nu u weet dat deze vragen helemaal niet willekeurig zijn, maar speciaal zijn gemaakt voor de ATPL-examen-database, is het tijd om u het systeem te laten zien. Om je analyse te beginnen, vraag je jezelf af: Liggen A en B op dezelfde meridiaan?
-

Algemene navigatie voor ATPL - Berekening van tracks en afstanden tussen twee willekeurige punten: Inleiding
In het ATPL-examen moet je rekenen tussen punten die er misschien uitzien als twee willekeurige posities op aarde, maar de waarheid is dat ze dat niet zijn. Deze punten zijn zorgvuldig gekozen zodat het probleem kan worden opgelost zonder de formules voor grootcirkelspoor en afstand te gebruiken.