Case 3 for GNAV two “random” points: When A and B are on the same latitude

Part 3 in the series about Calculating tracks and distances between two not so random points

On the bottom of this post you can try your luck with two ATPL questions for this case.

The plot thickens.

You must have arrived here because the answer to the two previous questions is “no”.

Case 1: Same meridian?

Case 2: Same anti-meridian?

Question 3:
Are A and B on the same latitude? = On the same parallel?

Example:

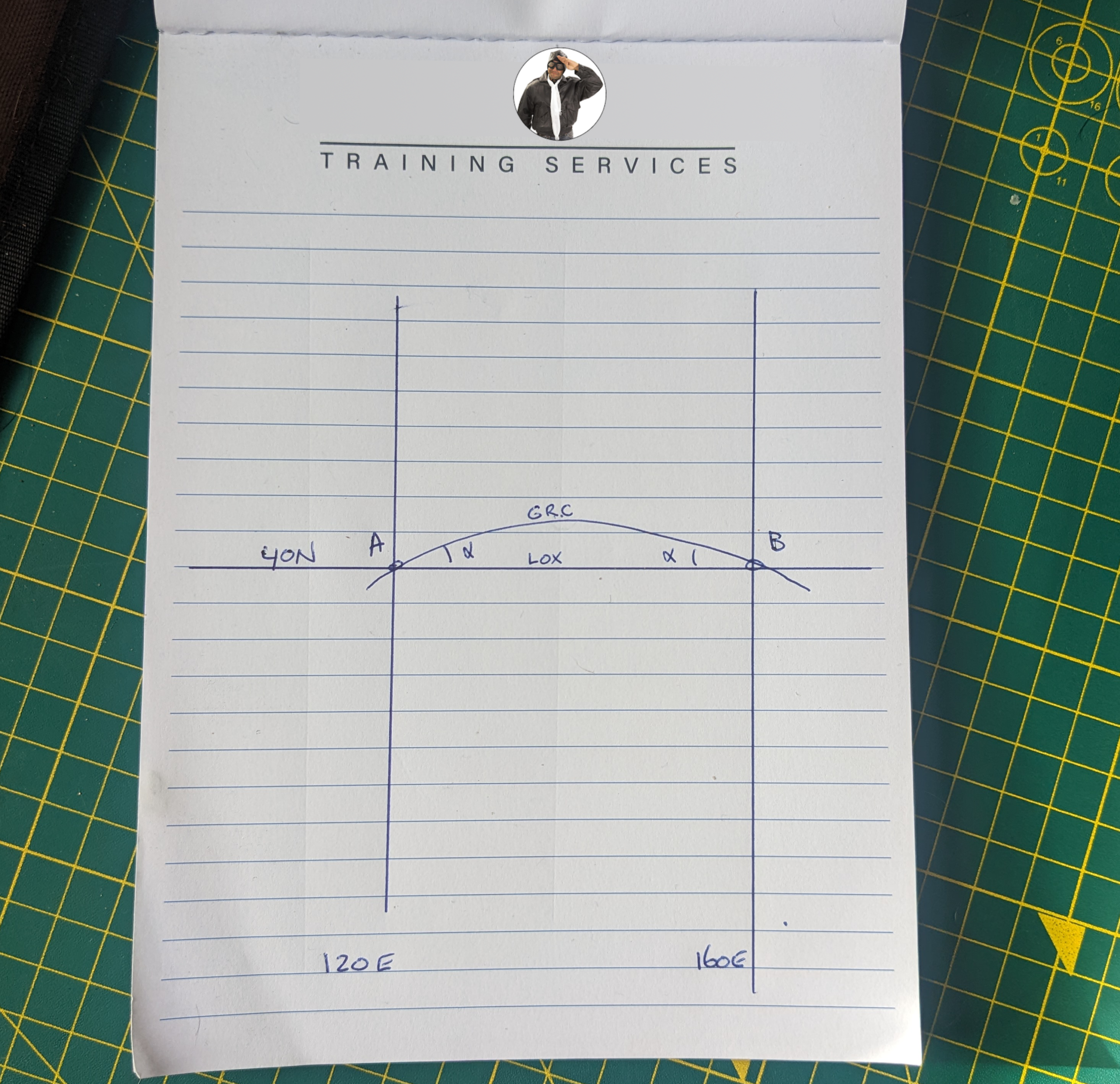
A 40N 120E
B 40N 160E

–> Yes. They are on the same latitude!
So they are also on the same parallel (40E). This is the same thing.

Skip to case 4 if this condition applies:

Are A and B at or past 70N or 70S?

Then skip to CASE 4! (will be published after this one.)

Solution:

Make a drawing

• Set up a picture of the two points in a Mercator projection.
• In a Mercator projection the parallel is a straight horizontal line.
  The parallel is a constant track line, also known as a rhumb line or loxodrome.
• Add the great circle. This looks like a curved line with the concave side to the equator.
• Add the angle between the great circle and the rhumb line.
  Let’s call it alpha (⍺)

Concave vs Convex

If you want to remember the difference between concave and convex then think of a cartoon cave that looks like a big black curved entrance where the concave side of the curve is the entrance.

Next step: Think about what the question wants you to answer and mark it in your drawing

You now have the setup that you need to answer questions like:

• What is the true track of the great circle from A to B in A?
• What is the true track of the great circle from A to B in B?
• What is the true track of the great circle from B to A in B?
• What is the distance of the rhumb line track from A to B?

With the formulas that you must know for ATPL and the data that this type of questions give you it is not possible to calculate the great circle distance between A and B. You will not get an exam question to do that.

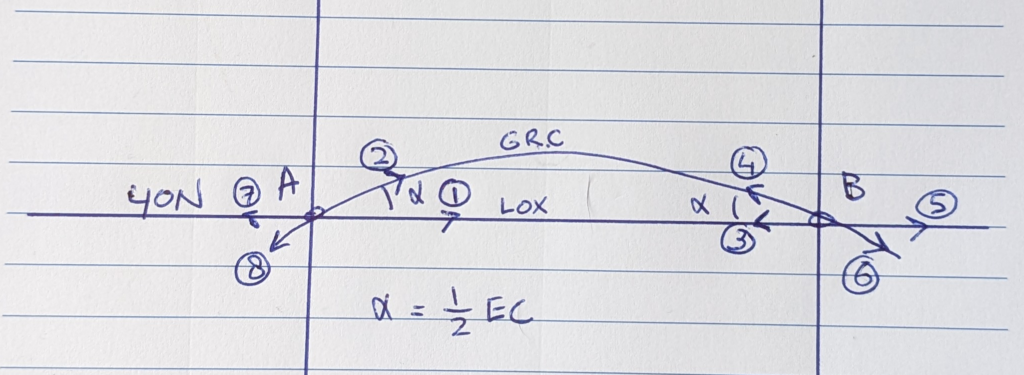
Remember: lox = loxodrome = rhumb line = constant track line

1. TTlox A to B -> EASY: 090
2. TTgrc A to B
3. TTlox B to A -> EASY: 270
4. TTgrc B to A in B
5. TTlox A to B in B -> EASY: 090
6. TTgrc A to B in B
7. TTlox B to A in B -> EASY:270
8. TTgrc B to A in A
9. Dlox or Rhumb line distance between A and B

Be careful!

Some of these are very easy. Too easy. The true track along a parallel is always 090 or 270. Make sure that you have your drawing set up correctly.

DO NOT ATTEMPT THIS EASY STUFF FROM MEMORY.
ALWAYS MAKE A DRAWING even if you think it is super simple because that is the moment where you start fucking up and spill points on your exam. Don’t say I didn’t warn you.

Also do not be fooled by a track that crosses the 180 meridian.
The track from 170E to 170W is to the east with 090 and not to the west (Shortest distance past the 180 meridian).

Great circles, earth’s convergence (EC) and conversion angle (CA)

The angle that we called ⍺ between the great circle and the rhumb line has a special name: It is called the conversion angle or CA.

The conversion angle (CA) is NOT THE SAME AS earth’s convergence (EC).
Do not confuse them.

There are two simple formulas for EC and CA.

A 40N 120E
B 40N 160E

EC =  CHlon x sin MEANlat
CHlon = Lon B – lon A = 160 – 120 = 40
MEANlat = Mean attitude A -> B = (Lon A + lon B)/2 = (40 + 40)/2 = 40
EC = 40 x sin40 = 25,7 degrees

CA = 1/2 EC
CA = 25,7/2 =12,9 degrees.
Note that I kept the digits in the calculator and only rounded CA after the final step.

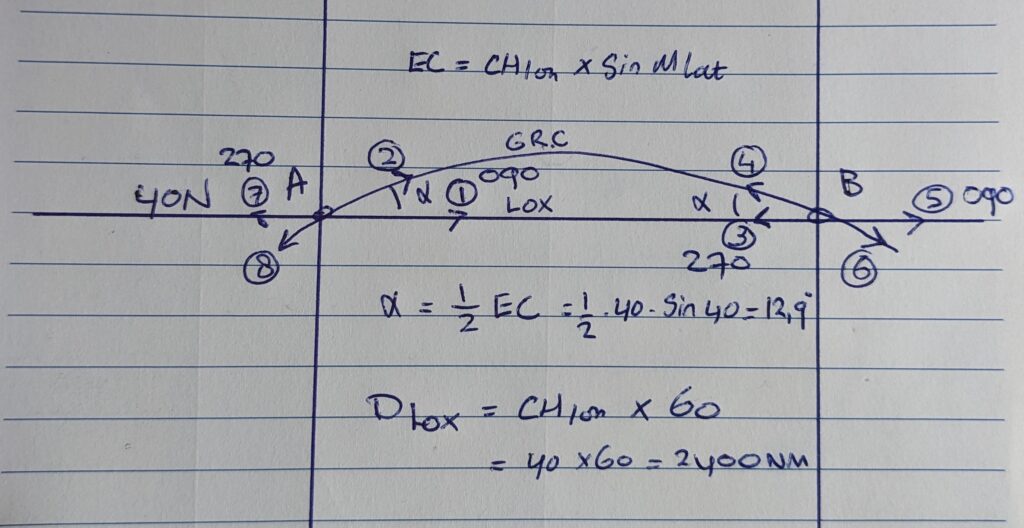
1. TTlox A to B = 090
2. TTgrc A to B = TTloxAB – ⍺ = 090 – 12,9 = 77,1 -> approximately 77.
3. TTlox B to A = 270
4. TTgrc B to A in B = TTloxBA + ⍺ = 270 + 12,9 = 282,9 -> approximately 283.
5. TTlox A to B in B = 090
6. TTgrc A to B in B = 090 + ⍺ = 090 + 13 = approximately 103.
7. TTlox B to A in B = 270
8. TTgrc B to A in A = 270 – ⍺ = 270 -13 = 257.
9. Dlox or Rhumb line distance between A and B = CHlong x 60 = 40 x 60 = 2400 NM.

Some notes and tips

Approximately

Most of the exam questions are using words like “approximately”. Like this:

“The great circle track measured at A from A to B is approximately:”

If you see this kind of wording then don’t worry too much about the number of decimals for ⍺ (CA). Just round it off to the nearest degree and you will find the answer.

USE YOUR CALCULATOR FOR EVERYTHING

Even for the silly calculations like 270 – 13.
The ATPL exam is a stressful thing and you can use al the help you can get. That includes your calculator.
Do not be an idiot. If you don’t use your calculator you will make silly mistakes and they will cost you points. Trust me, I’ve seen it many times.

That’s it for now.
The next post will be about what to do when all else fails. It will be interesting.

Try these ATPL questions

11

Created on November 27, 2022 By Paul

Try these ATPL questions

1 / 2

Q12911 – The great circle track measured at A (45º00’N 010º00’W) from A to B (45º00’N 019º00’W) is approximately:

093

273

090

270

2 / 2

Q14256 – Position A = (56º00.0”S, 163º57.2”E) Position B = (56º00.0”S, 171º47.4”W) For the route from A to B the;

great circle direction at B is 100.1º

great circle direction at B is 080.7º

rhumb line distance is 1455.4 NM

rhumb line distance is 1206.6 NM

Your score is

The average score is 4%

LinkedIn Facebook Twitter

0%

Restart quiz