Category: GNAV
-
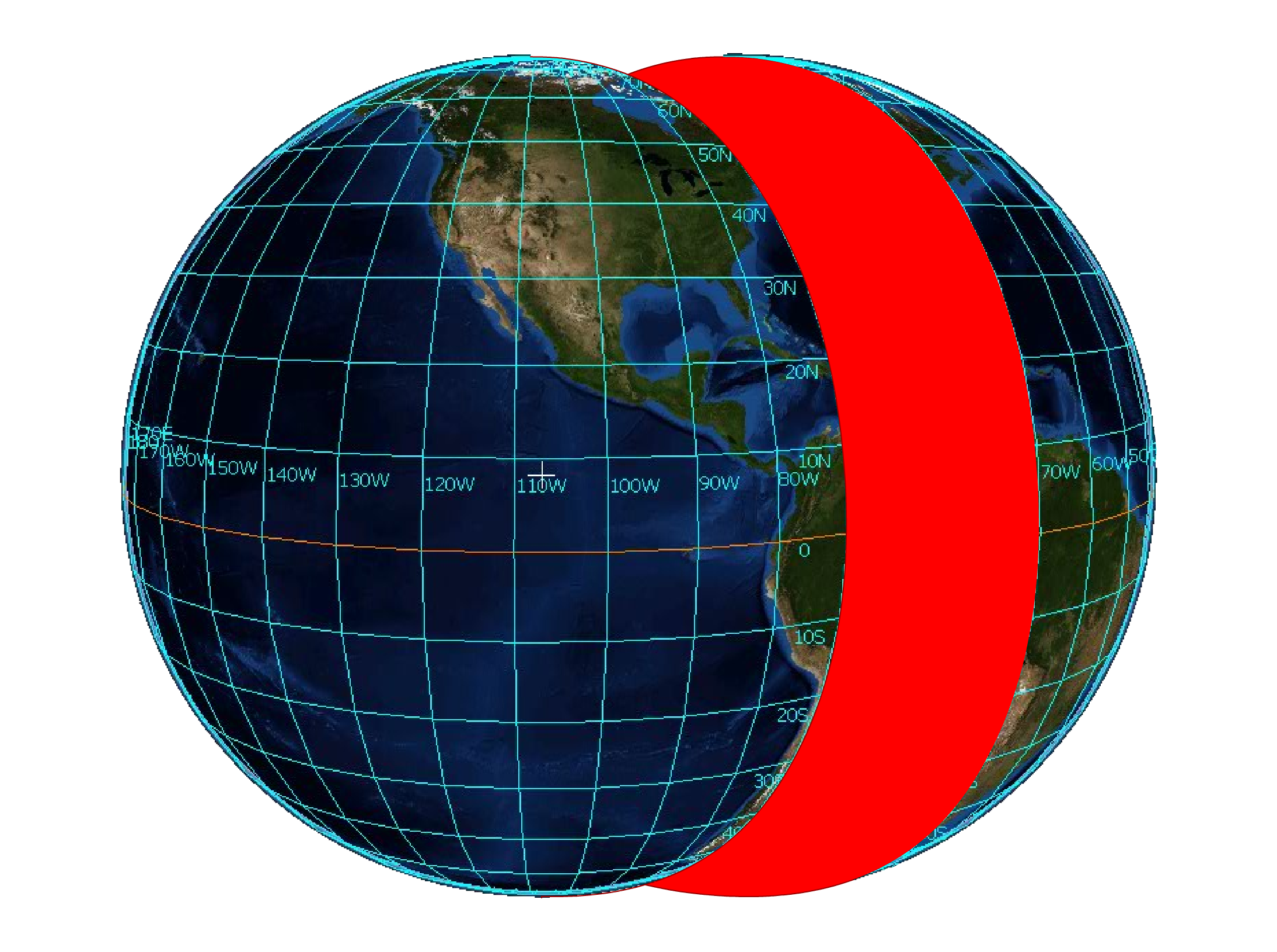
Case 4 – EASA ATPL General Navigation calculations between two “random” points: Find the triangle
If you want to calculate track and/or distance for an EASA General navigation exam question without using the classic great circle formulas and after all the other shortcuts have failed then you must find the triangle in the lines that connect the two coordinates.
-

Case 3 for GNAV two “random” points: When A and B are on the same latitude
Part 3 in the series about Calculating tracks and distances between two not so random points On the bottom of this post you can try your luck with two ATPL questions for this case. The plot thickens. You must have arrived here because the answer to the two previous questions is “no”. Case 1: Same…
-

Case 2 for GNAV two “random” points: A and B are on the anti-meridian
If case 1 is not true then try this: Question 2:Are A and B on each other’s anti-meridian? Anti-meridians are two meridians exactly 180 degrees apart that connect a great circle around the globe. Example: A: 40N 120EB: 10N 060W
-
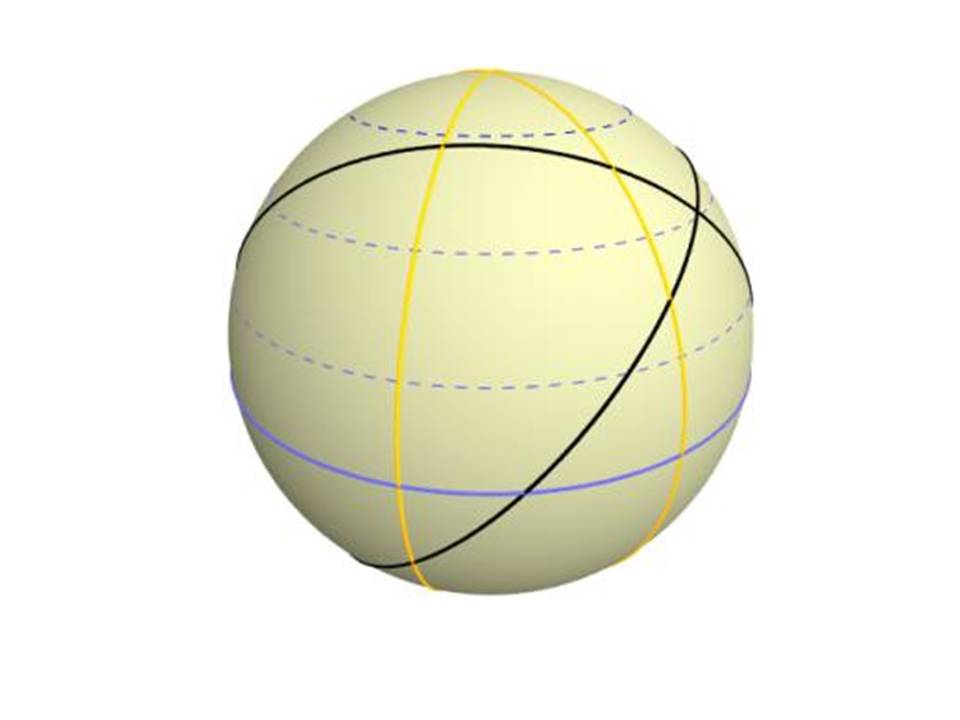
Case 1 for GNAV two “random” points: A and B are on the same meridian
So now that you know that these questions not random at all but specifically crafted for the ATPL exam-database it is time to show you the system. To start your analysis, ask yourself: Are A and B on the same meridian?
-

General Navigation for ATPL – Calculating tracks and distances between two random points: Introduction
In the ATPL exam you must calculate between points that may look like they are just two random positions on earth, but the truth is that they are not. These points have been carefully selected so that the problem can be solved without using the formulas for great circle track and distance.