Case 4 – EASA ATPL General Navigation calculations between two “random” points: Find the triangle

General navigation for ATPL – Find the triangle

I told you there is a system in the madness.

If you want to calculate track and/or distance for an EASA General navigation exam question without using the classic great circle formulas and after all the other shortcuts have failed then you must find the triangle in the lines that connect the two coordinates.

How computers do it

Before JAR-FCL took over the ATPL exams in Europe around the year 2000, you would remember the formulas for great circles, go to the exam, insert the coordinates of A and B into them and presto! Bob’s your uncle.

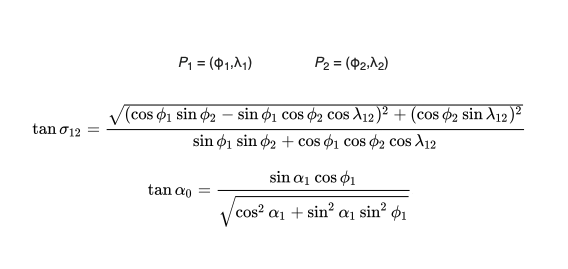
The EASA way, how the ATPL exam does it

Fast forward to today. The EASA syllabus does not want you to learn the formulas for track and distance of a random great circle but they still want you to calculate tracks and distances. This is an interesting dilemma. The question writers must now find a way to make it look like General Navigation.

There are however some shortcuts and they allow you to calculate tracks and distances by simplifying them along meridians and parallels. That is, if you are lucky that the coordinates are both actually on the same meridian or parallel. Like this:

If these 3 cases do not apply you can use a method that I call “Find the triangle”. Usually when you end up here we are dealing with two positions that are in the polar regions. 70N or 70S or beyond.

Where is the triangle?

To have a triangle you need 3 lines. The great circle track is just one of them. The other two are usually meridians. Like this:

What is in the triangle?

The meridians are obvious, they are the two legs of the triangle. The dotted line is a straight line that completes it. Could be a track between two points.
Inside a triangle all the angles count up to 180 degrees and you can do some basic calculations to find the length of each leg.

Does it look familiar yet? You may recognise this as a POLAR STEREOGRAPHIC PROJECTION.

Look at this question from the European question bank:

This is what it looks like in a drawing.
You may notice that I draw the great circle from A to B as a straight line. This is close enough and you will find the correct answer.
In reality a great circle it is not a straight line in a polar stereographic projection but in our case this is close enough. There is in fact a slight curve concave to the pole but that’s a long story that I’m not going to cover here.

• Initial track is the requested answer.
• Inside the triangle the angles all add up to 180.
• ⍺1 = the difference in longitude between A and B = 120º
• There is now still 180 – 120 = 60º remaining in the triangle
• Looks like Initial Track and ⍺2 are equal so that would mean that are each 30º

How to proof that? –>
Well, it “happens” to be the case that the two legs of the triangle from the north pole to A and from the north pole to B are of equal length. As a result, the angles that they enclose are equal.
There’s the proof we need. Initial track = 030º.

Other variants to use this theme

Distances from ground features or beacons

A few very nasty questions exist that have basically nothing to do with navigation other than the words distance and bearing or even aircraft in them. In these questions you fly a track and a few minutes later the bearing to a feature happens to be part of a triangle with a 90 degree angle and two equal legs. They then want to know for instance the distance to the feature which happens to be equal to the distance travelled. Please.
It’s been a while so hopefully these questions have been deleted from the databases by now. What can I say.
Draw the tracks, you will see the triangle.

Approximately is the give-away

The word “approximately” means there is probably a triangle or some rule of thumb involved. The answer that you get is an approximation of the actual value.

• Two points that are on different parallels and different meridians but only a few degrees N or S apart are likely to form a triangle somewhere. This is also possible on a Mercator-projection near the equator.
• If you draw a triangle and you find a 90 degree angle then the solution is close-by.
• Some of the biggest headaches of GNAV for ATPL: Gridded charts in polar regions are a well known source of questions that contain triangles. The difference in longitude between the two points is usually a good starting point for your calculations.

2

Created on December 06, 2022 By Paul

Find the triangle

1 / 6

Q876 – On a polar stereographic projection chart showing the South Pole, a straight line joins position A (70ºS 065ºE) to position B (70ºS 025ºW). The true course on departure from position A is approximately:

315º

250º

135º

225º

2 / 6

Q3337 – An aircraft obtains a relative bearing of 315º from an NDB at 0830. At 0840 the relative bearing from the same position is 270º. Assuming no drift and a GS of 240 kt, what is the approximate range from the NDB at 0840?

30 NM

50 NM

60 NM

40 NM

3 / 6

Q4923 – Given: An aircraft is flying a track of 255º(M), 2254 UTC, it crosses radial 360º from a VOR station, 2300 UTC, it crosses radial 330º from the same station. At 2300 UTC, the distance between the aircraft and the station is:

less than it was at 2254 UTC

greater than it was at 2254 UTC

randomly different than it was at 2254 UTC

the same as it was at 2254 UTC

4 / 6

Q4326 – An island is observed to be 15º to the left. The aircraft heading is 120º(M), variation 17º(W). The bearing º(T) from the aircraft to the island is:

122

088

268

302

5 / 6

Q4325 – A ground feature was observed on a relative bearing of 315º and 3 MIN later on a relative bearing of 270º. The W/V is calm; aircraft GS 180 kt. What is the minimum distance between the aircraft and the ground feature?

3 NM

12 NM

9 NM

6 NM

6 / 6

Q1527 – The Great Circle bearing from A (70ºS 030ºW) to B (70ºS 060ºE) is approximately:

132º(T)

048º(T)

090º(T)

312º(T)

Your score is

The average score is 1%

LinkedIn Facebook Twitter

0%

Restart quiz