Let’s make some sense of the EASA exam for General Navigation
A lot of people are struggling to pass the General Navigation exam for the ATPL license. Now obviously this is because it is hard but let’s now overcomplicatie things.
There are ways to analyse the questions to remove some of the headache.
You have a bunch of formulas for conversion angle, departure, earth’s convergency and great circle distance with which you are supposed to calculate tracks and distances between two random points.
Two random points. Really?
Well let me just spoiler it for you straight away:
They may look like they are just two random positions on earth, but the truth is that they have been carefully selected to avoid the following:
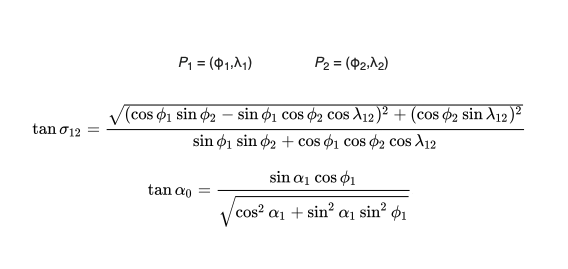
Formulas: Wikipedia
The two formulas that you see here allow you to calculate tracks and distances between any two points on a globe. If you just learn how to remember and use them we could now start by solving a few sample problems and be done with it. The truth is that since the start of EASA ATPL exams around the year 2000 it was decided that they are not in the learning objectives.
Pilot’s brains need not explode from this stuff any longer. But this introduces a new problem:
If the two track points can not be random, then how can the exam present problems that a pilot can solve?
And there it is!
Once you know that the questions are NEVER random, then there must be a system behind them that avoids using the great circle formulas.
This system does indeed exist.
To solve all the ATPL questions about track or distance between two points, all you have to do is follow a short list of possibilities and then the way to solve it will always present itself.
In the next few posts I will guide you through all the options. I will explain how to apply them to example questions from the ATPL question bank that have given many of my past students headaches. After this you will not only be able to figure out where to even start with the queston but also how to solve it.
There are some things that you should already know by now from your GNAV studies
If you made it this far in your effort to master General Navigation for the Air Transport License then you already know a couple of important basics. At least, that’s what your teacher says. Do you even have a teacher or are you being victimized by one of those computer based training programs? I feel your pain.
Anyway, here is a list of stuff that should make some sense to you:
The shortest distance between two points on a globe is a great circle
About great circles:
- A great circle can connect any two points on the globe
- A great circle is actually a straight line on a globe, just like a rubber band around a ball.
- A great circle does NOT have a constant track
- Except when the great circle is also following a meridian of longitude or the equator
- The track of the great circle changes due to the convergence of the meridians
- On some maps a great circle looks like a straight line while on others it has a massive curvature.
If you wrap a rubber band around a toy globe it becomes obvious how great circles compare to rhumb lines
A line with a constant track is called a loxodrome or a rhumb line
- A rhumb line can connect any two points on the globe
- A rhumb line has a constant track by definition, this is why a meridian and the equator are at the same time great circle tracks and rhumb lines
- A parallel of latitude is always a rhumb line
- A rumb line is most often not the shortest distance
- Only when the rhumb line also follows a meridian or the equator it is the shortest distance.
- On some maps a rhumb line looks like a straight line while on others it has a massive curvature.
Here are some typical GNAV ATPL exam questions, try them:
This is the first post in a short series that I wil publish here. Follow me along as they come online.

